哈希算法是计算机以及互联网发展过程中最基本的算法之一了,有意无意的,所有计算机行业从业者,都或多或少的接触过这些算法,并享受着其带来的种种便利。这包括网络传输中消息的传输,隐私信息的保护,编程语言中的字典,图片、地理位置的搜索,信息的分布式存储等等。如大多数基础的算法和技术一样,哈希技术隐于人们的眼皮之下,虽得见但却鲜受关注。
但是,我们又必须意识到,正是由于哈希算法在计算机领域中的基础作用,其优势、缺陷、安全性、性能的考量往往能极大的影响一个项目,一个产品甚至行业的发展走向。
就我们常见的几种哈希算法,这里进行一下分类和讨论。
何谓哈希
哈希,是指对数据使用某种散列函数,生成指定长度代码序列的过程,这种代码序列,我们称为哈希码,使用的散列函数被称为哈希算法。哈希码代表着数据的某种特性,其特点包括:
- 压缩性(有限解空间),目前使用的大多数哈希码,为64、128、256位字符串,其解空间也有$2^{64}$、$2^{128}$、$2^{256}$个值;
- 不可逆,所有的哈希算法都是一种1->n的映射,一般情况下,n趋于无限大,这使得由数据计算哈希码可行,而由哈希码计算出原数据不可行,这个特性,使哈希函数得以成为数据安全校验的基础;
- 随机均匀,数据的哈希码在其解空间中能呈均匀分布,相似的数据生成的哈希码无关联性(除后面所说的部分相似性哈希算法),即无法通过哈希值,推测原数据的一部分,这个特性是数据防篡改,字典等的基础。
不同类的哈希算法,还会有其不同的特性。
随机哈希:沉默的劳动者
平常接触的最多的也就是这类算法,也是最被忽视的一类算法,其中以md5-sha系列算法为代表,经过若干次安全性迭代,主要增强其防碰撞方面的特性。
特性包括但不限于:
- 抗碰撞,指对于不同的数据,生成的哈希码相同的概率低,对于作为摘要作用的算法,其抗碰撞性的要求是及其严苛的。
- 抗分析,指无法通过哈希码,反推数据及数据本身。
- 均匀性,指在对于任一数据,其哈希码在被计算出之前,落在其值域中的任一值上的概率是相同的。
其使用场景及一些常见问题的解决办法:
- 字典数据结构,作为编程人员最常用的数据结构之一,也被称为散列表,特点为查找时间复杂度为常数级,但有比较高的空间复杂度,实际使用中,会只使用哈希码的一个子集,允许轻微碰撞,来降低空间消耗,当出现碰撞后,解决碰撞的办法有开放地址法和拉链法。
- 数据安全传输,数据传输过程需要保证数据篡改及数据不完整,而防窃听由加密算法保证,二者常常一起使用,这种用途的哈希算法,也被称为摘要算法,数据加密时,会同时写入数据的哈希码,数据不完整或者被篡改后,生成的哈希码都会产生变化,接收者通过校验哈希码,即可知道数据是否发生了变化。
- 用户口令安全性保存,多次爆出的服务器被拖库事件使我们意识到,服务器也无法完全保证用户口令的安全,最安全的办法,就是服务器也不保存用户口令,而只保留必要的鉴权要素。初级策略是保存口令的哈希码,但据统计,超过大半数的用户使用常用密码,密码容易被通用彩虹表破解;次级策略是服务端持盐,保存加盐口令的哈希码,但是对于大量使用相同口令的用户,其加盐口令的哈希码相同,攻击者碰撞出其中一个用户的口令,即攻破了所有使用相同口令用户的权限;三级策略是服务端保存用户随机盐及用户加盐口令的哈希值,则攻击者需要逐个破解每个用户的口令,难度要大得多。
- 分布式数据存储节点选择,主要依靠哈希算法均匀性特点,节点选择算法为hash(data)%N,N为节点个数,这种算法无法满足集群动态伸缩的需要,解决办法为后面会提到的一致性哈希算法。
相似性哈希算法:近邻数据搜索专家
我们最常接触的图片搜索,地理位置附近搜索都属于此类算法。
但与随机哈希不同的是,相似性哈希算法并不具有明显的均匀性,相反,相似的数据应该具有相似哈希码。相似性哈希算法特征:
- 压缩性,相似性哈希算法使用哈希码作为数据的特征,来进行搜索,哈希码解空间应具有相当程度的限制来支持索引。
- 关联性,相似性哈希码应具有关联性,使得具有相似特征的数据生成的哈希码也相似。
进行相似性数据搜索,涉及两个关键过程:特征值提取,近邻搜索,搜索算法与特征值提取算法过程相关,而特征值的提取,因数据特性的不同而不同。
图片搜索
特征提取时,我们关注图片的频率域的处理,频率代表图片灰度上的变化快慢,高频为图像边缘,低频为图像主体面貌,因此特征值提取算法需要获取的是低频信息,特征提取得到的哈希码也称为图片的指纹,常见的特征值提取算法有:
1 | (1). 均值哈希算法: |
地理位置搜索
使用GeoHash算法,用于将二维地理位置转化为字符串,通过比较字符串的值,即可知道地理位置间的距离。GeoHash算法,将二维数据转化为以为数据,从而使得地理位置索引成为可能。
GeoHash算法包含两个过程:
- 编码过程:该过程对二维地理位置分别进行编码,编码过程是迭代的,每一轮迭代,将编码区间平分成两个子区间,根据位置所处的子区间,编码末位增加0或1,然后对两部分区间迭代进行下一轮编码,直至编码达到所需长度,经度纬度的初始区间分别为[0,180]、[-90,90]。
如对点P(m,n)水平纬度进行编码,第k+1轮迭代时,编码区间为[A,B),此时编码为$a_{1}a_{2}a_{3}…a_{k}$,而$m\in[A,B)$,将编码区间分成[A,$\frac{A+B}{2}$),[$\frac{A+B}{2}$,B)两部分,若$m<\frac{A+B}{2}$,则编码变为$a_{1}a_{2}a_{3}…a_{k}0$,进入[A,$\frac{A+B}{2}$)区间进行迭代,否则编码变为$a_{1}a_{2}a_{3}…a_{k}1$,进入[$\frac{A+B}{2}$,B)区间迭代。
- 组码过程:该过程将地理位置两个纬度分别生成的编码进行组合,如水平纬度的编码放置到奇数位,纵向纬度编码放置到偶数位,组码生成的编码以四个为一组,映射为0-9|b-z(去除a,i,l,o),生成base32编码,此为编码过程,解码过程于此相反。
产生的编码长度反映了地理为值搜索的精度,长度越长,精度越高,就实际使用情况来看,编码长度为9时,精度可以达到2m,已经满足大多数情况下的需要了.计算两个编码位置间的距离的时候,只需比较两个编码之间的距离。
GeoHash在实施时,需要考虑两个问题。
1.上述编组码的过程,并不是均匀的,表现出明显的空间突变性。
1 | +-------------+--------------+ +--------+--------+--------+--------+ +-------------+--------------+ |
实际上,以两位为一组进行迭代的所有编码方式,都存在一定的突变型,还有一些编组码方式,在迭代过程中,加入一些旋转动作,以4位或更大的单位进行迭代,这包括

其中以Hilbert对于空间突变性的处理效果最优异,这是一种以8位为一组的迭代编码方式,其中这8位组成一个3阶曲线,包含4段2阶曲线,每个2阶曲线又包含4段1阶曲线,1阶曲线向2阶曲线过渡的方式与2阶曲线向3阶曲线过渡的方式相同
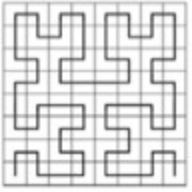
2.编码和组码产生的编码实际表示的是一个矩形的区域,而不是没有面积的点,那么处于边界上的点,在计算的时候会产生精度内误差:处于同一块内相对边界上的两点,实际距离要大于相邻块上共同边界上的两点,尽管前者的编码相同,而后者的编码不同。为解决这种问题,搜索时往往不将编码作为唯一评判依据,而是在目标点附近扩大搜索,对进入搜索范围的点,计算真实距离,根据真实距离筛选出所需要的结果。
一致性哈希算法:分布式集群稳定性的保障
前面提到在分布式集群中进行节点查找的方法,但是分布式关心的是集群的稳定性,这种稳定性可以通过增加节点的方式来增强,单节点的运行环境并不能被保证,可以说,集群是一个不断变化的容器,取模定位的方法中引入来集群节点数变量,使得节点查找无法保证单调性,以增加一个节点为例,集群中节点数由N变化为N+1时,原第k个节点将有$\frac{k}{N+1}-\frac{k-1}{N}=\frac{N+1-k}{N(N+1)}$的数据量保持有效,整个集群共$\sum\limits_{k=1}^{N}\frac{N+1-k}{N(N+1)}=\frac{1}{2}$的数据保持有效,也就是说每次增加一个节点后,整个集群将有一半的数据因节点查找而失效。试想一下,如果是一个庞大分布式缓存集群,一半数据失效,失效数据请求将全部击中底层持久化数据载体,瞬间流量将呈上百倍的增加,对于整个服务的稳定性,无疑是极大的考验。
一致性哈希算法的主要用途即是适应集群这种动态扩展的环境,其原理是
1 | 1. 一致性哈希算法哈希码的解空间被组织成一个环状结构 |
可以看到,每一次节点的增减,只会影响到一个节点的数据变化,相对于取模定位的方式,集群动态变化对节点查找失效的影响小来很多。
但是,对于取模的方式,无论节点怎么变化,最终经过重新哈希后,各节点承担的数据量是相同的,而一致性哈希算法即使在最初节点节点分布均匀的情况下,经过节点增减,受影响节点承担数据量或减少或增加,整个集群中数据呈现出不均匀的分布。为了解决均匀性的问题,一致性哈希算法增加了虚拟节点,每个真实节点虚拟出若干各节点,挂载到哈希环中不同位置,这样节点增减后,数据的变化将分布到不同的节点中,无论是数据均匀性,还是单节点的压力状况都能得到缓解。虚拟节点越多,这种效果越好。
1 | Hash(data) (E) |